Khinchin's Constant on:
[Wikipedia]
[Google]
[Amazon]
In
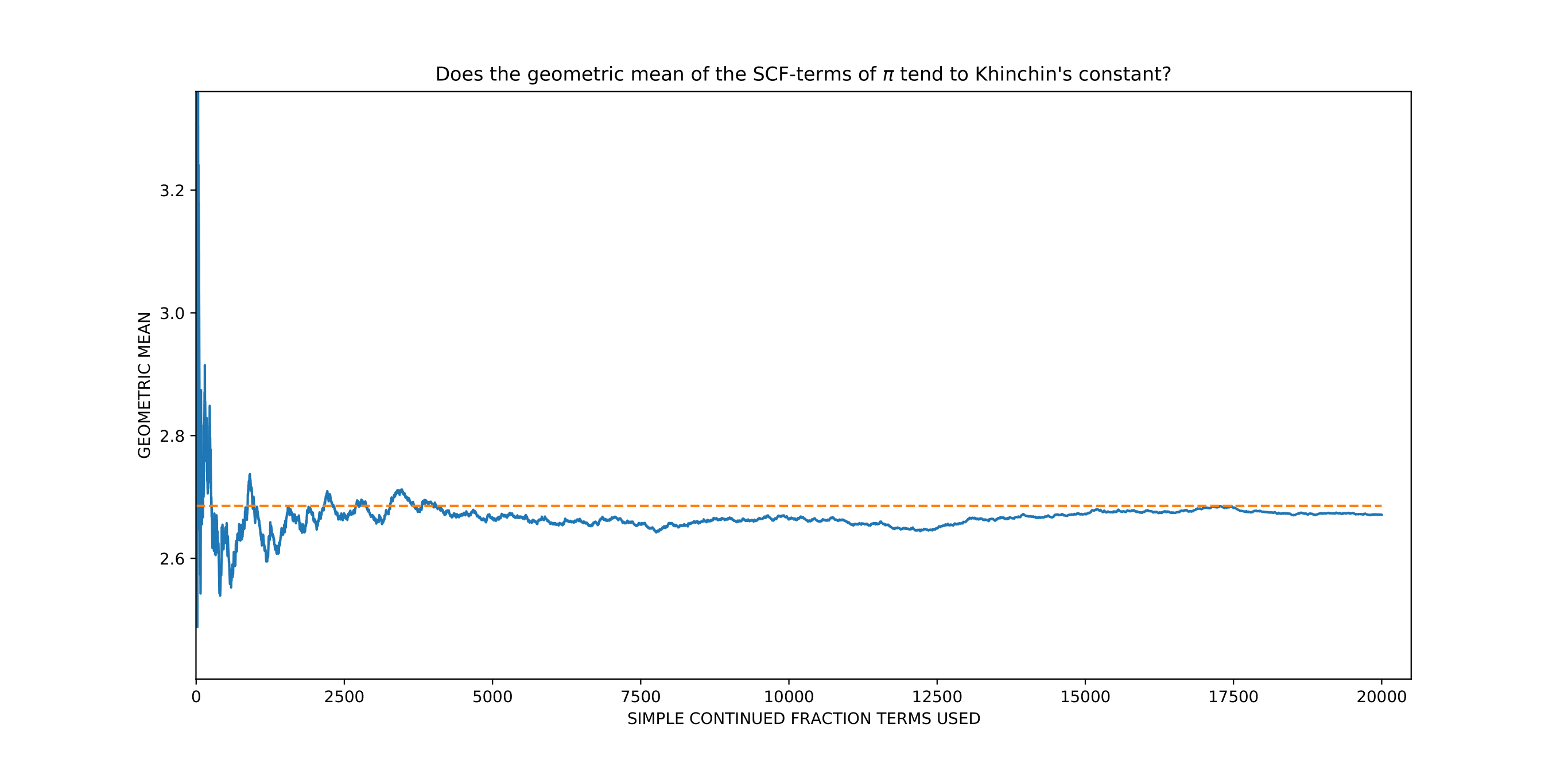 * , the
* , the
110,000 digits of Khinchin's constant
10,000 digits of Khinchin's constant
Continued fractions Mathematical constants Infinite products
number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mat ...
, Aleksandr Yakovlevich Khinchin proved that for almost all real numbers ''x'', coefficients ''a''''i'' of the continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer ...
expansion of ''x'' have a finite geometric mean that is independent of the value of ''x'' and is known as Khinchin's constant.
That is, for
:
it is almost always
In probability theory, an event is said to happen almost surely (sometimes abbreviated as a.s.) if it happens with probability 1 (or Lebesgue measure 1). In other words, the set of possible exceptions may be non-empty, but it has probability 0. ...
true that
:
where is Khinchin's constant
:
(with denoting the product over all sequence terms).
Although almost all numbers satisfy this property, it has not been proven for ''any'' real number ''not'' specifically constructed for the purpose. Among the numbers whose continued fraction expansions apparently do have this property (based on numerical evidence) are π, the Euler-Mascheroni constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma ().
It is defined as the limiting difference between the harmonic series and the natural l ...
γ, Apéry's constant
In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number
:
\begin
\zeta(3) &= \sum_^\infty \frac \\
&= \lim_ \left(\frac + \frac + \cdots + \frac\right),
\end
...
ζ(3), and Khinchin's constant itself. However, this is unproven.
Among the numbers ''x'' whose continued fraction expansions are known ''not'' to have this property are rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rat ...
s, roots of quadratic equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where represents an unknown value, and , , and represent known numbers, where . (If and then the equation is linear, not q ...
s (including the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0,
where the Greek letter phi ( ...
Φ and the square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
s of integers), and the base of the natural logarithm ''e''.
Khinchin is sometimes spelled Khintchine (the French transliteration of Russian Хинчин) in older mathematical literature.
Sketch of proof
The proof presented here was arranged byCzesław Ryll-Nardzewski
Czesław Ryll-Nardzewski (; 7 October 1926 – 18 September 2015) was a Polish mathematician.
Born in Wilno, Second Polish Republic (now Vilnius, Lithuania), he was a student of Hugo Steinhaus. At the age of 26 he became professor at Warsaw Uni ...
and is much simpler than Khinchin's original proof which did not use ergodic theory.
Since the first coefficient ''a''0 of the continued fraction of ''x'' plays no role in Khinchin's theorem and since the rational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rat ...
have Lebesgue measure zero, we are reduced to the study of irrational numbers in the unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1. It is often denoted ' (capital letter ). In addition to its role in real analysis ...
, i.e., those in . These numbers are in bijection with infinite continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer ...
s of the form ; ''a''1, ''a''2, ... which we simply write 'a''1, ''a''2, ... where ''a''1, ''a''2, ... are positive integers. Define a transformation ''T'':''I'' → ''I'' by
:
The transformation ''T'' is called the Gauss–Kuzmin–Wirsing operator. For every Borel subset
In mathematics, a Borel set is any set in a topological space that can be formed from open sets (or, equivalently, from closed sets) through the operations of countable union, countable intersection, and relative complement. Borel sets are nam ...
''E'' of ''I'', we also define the Gauss–Kuzmin measure of ''E''
:
Then ''μ'' is a probability measure on the ''σ''-algebra of Borel subsets of ''I''. The measure ''μ'' is equivalent
Equivalence or Equivalent may refer to:
Arts and entertainment
*Album-equivalent unit, a measurement unit in the music industry
* Equivalence class (music)
*'' Equivalent VIII'', or ''The Bricks'', a minimalist sculpture by Carl Andre
*''Equiva ...
to the Lebesgue measure on ''I'', but it has the additional property that the transformation ''T'' preserves
Fruit preserves are preparations of fruits whose main preserving agent is sugar and sometimes acid, often stored in glass jars and used as a condiment or spread.
There are many varieties of fruit preserves globally, distinguished by the meth ...
the measure ''μ''. Moreover, it can be proved that ''T'' is an ergodic transformation of the measurable space
In mathematics, a measurable space or Borel space is a basic object in measure theory. It consists of a set and a σ-algebra, which defines the subsets that will be measured.
Definition
Consider a set X and a σ-algebra \mathcal A on X. Then the ...
''I'' endowed with the probability measure ''μ'' (this is the hard part of the proof). The ergodic theorem
Ergodic theory (Greek: ' "work", ' "way") is a branch of mathematics that studies statistical properties of deterministic dynamical systems; it is the study of ergodicity. In this context, statistical properties means properties which are expres ...
then says that for any ''μ''-integrable function
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with d ...
''f'' on ''I'', the average value of is the same for almost all :
:
Applying this to the function defined by ''f''( 'a''1, ''a''2, ... = log(''a''1), we obtain that
:
for almost all 'a''1, ''a''2, ...in ''I'' as ''n'' → ∞.
Taking the exponential
Exponential may refer to any of several mathematical topics related to exponentiation, including:
*Exponential function, also:
**Matrix exponential, the matrix analogue to the above
*Exponential decay, decrease at a rate proportional to value
*Expo ...
on both sides, we obtain to the left the geometric mean of the first ''n'' coefficients of the continued fraction, and to the right Khinchin's constant.
Series expressions
Khinchin's constant may be expressed as arational zeta series In mathematics, a rational zeta series is the representation of an arbitrary real number in terms of a series consisting of rational numbers and the Riemann zeta function or the Hurwitz zeta function. Specifically, given a real number ''x'', t ...
in the form
:
or, by peeling off terms in the series,
:
where ''N'' is an integer, held fixed, and ζ(''s'', ''n'') is the complex Hurwitz zeta function
In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables with and by
:\zeta(s,a) = \sum_^\infty \frac.
This series is absolutely convergent for the given values of and and c ...
. Both series are strongly convergent, as ζ(''n'') − 1 approaches zero quickly for large ''n''. An expansion may also be given in terms of the dilogarithm
In mathematics, Spence's function, or dilogarithm, denoted as , is a particular case of the polylogarithm. Two related special functions are referred to as Spence's function, the dilogarithm itself:
:\operatorname_2(z) = -\int_0^z\, du \textz ...
:
:
Hölder means
The Khinchin constant can be viewed as the first in a series of theHölder mean
In mathematics, generalized means (or power mean or Hölder mean from Otto Hölder) are a family of functions for aggregating sets of numbers. These include as special cases the Pythagorean means (arithmetic, geometric, and harmonic means).
D ...
s of the terms of continued fractions. Given an arbitrary series , the Hölder mean of order ''p'' of the series is given by
:
When the are the terms of a continued fraction expansion, the constants are given by
:
This is obtained by taking the ''p''-th mean in conjunction with the Gauss–Kuzmin distribution
In mathematics, the Gauss–Kuzmin distribution is a discrete probability distribution that arises as the limit probability distribution of the coefficients in the continued fraction expansion of a random variable uniformly distributed in (0,&nbs ...
. For example, the harmonic mean (''p'' = −1) of the terms of a continued fraction is almost always
: .
The value for ''K''0 is obtained in the limit of ''p'' → 0.
Open problems
 * , the
* , the Euler–Mascheroni constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma ().
It is defined as the limiting difference between the harmonic series and the natural l ...
γ, and Khinchin's constant itself, based on numerical evidence, are thought to be among the numbers whose geometric mean of the coefficients ''a''''i'' in their continued fraction expansion tends to Khinchin's constant. However, none of these limits have been rigorously established.
* It is not known whether Khinchin's constant is a rational, algebraic irrational
Irrationality is cognition, thinking, talking, or acting without inclusion of rationality. It is more specifically described as an action or opinion given through inadequate use of reason, or through emotional distress or cognitive deficiency. T ...
or transcendental number.
See also
* Lochs' theorem * Lévy's constant *List of mathematical constants
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a symbol (e.g., an alphabet letter), or by mathematicians' names to facilitate using it across multiple mathematical problems. For exa ...
References
External links
{{Commons category, Khinchin's constant110,000 digits of Khinchin's constant
10,000 digits of Khinchin's constant
Continued fractions Mathematical constants Infinite products